KerrGeodesics

The KerrGeodesics package for Mathematica provides functions for computing timelike geodesics and their properties in Kerr spacetime.

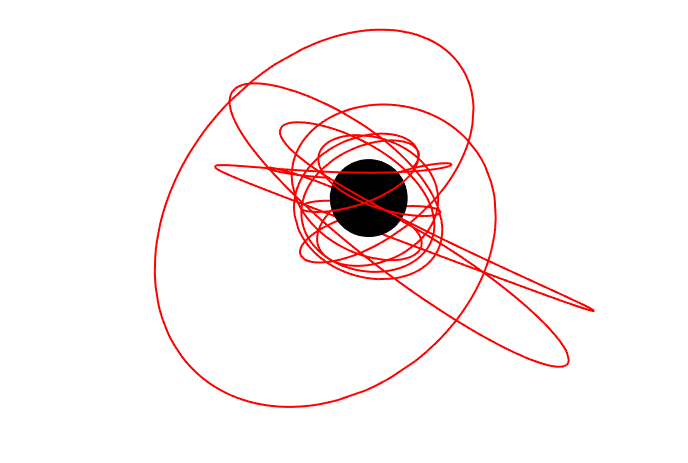
Example usage

As a quick example, the figure at the top of this page is made using the simple commands:

orbit = KerrGeoOrbit[0.998, 3, 0.6, Cos[π/4]];
{t, r, θ, φ} = orbit["Trajectory"];

Followed by the plot command:

Show[
 ParametricPlot3D[{r[λ] Sin[θ[λ]] Cos[φ[λ]], r[λ] Sin[θ[λ]] Sin[φ[λ]], r[λ] Cos[θ[λ]]}, {λ, 0, 20}, 
  ImageSize -> 700, Boxed -> False, Axes -> False, PlotStyle -> Red, PlotRange -> All],
 Graphics3D[{Black, Sphere[{0, 0, 0}, 1 + Sqrt[1 - 0.998^2]]}]
 ]

Orbital parametrization

The orbits are parameterized by the following

$a$ - the black hole spin
$p$ - the semi-latus rectum
$e$ - the eccentricity
$x_\text{inc} = \cos\theta_\text{inc}$ - the orbital inclination.

The parametrization $\{a,p,e,\theta_\text{inc}\}$ is described in, e.g., Sec. II of arXiv:gr-qc/0509101.

The package currently supports bound orbits and hyperbolic orbits ($e > 1$). Plunging orbits are coming in a future release.

Orbital constants and frequencies

The constants of the motion can be computed using

KerrGeoEnergy[a,p,e,x]
KerrGeoAngularMomentum[a,p,e,x]
KerrGeoCarterConstant[a,p,e,x]

The above three can be computed together using KerrGeoConstantsOfMotion[a,p,e,x].

The orbital frequencies (w.r.t Boyer-Lindquist time $t$) are computed using KerrGeoFrequencies[a,p,e,x]. For this function you can pass the option Time->"Mino" to compute the frequencies w.r.t. Mino time.

Special orbits

The package allows you compute a variety of special orbits including the innermost stable circular/spherical orbit (ISCO/ISSO), innermost bound spherical orbit (IBSO), the photon orbit and the location of the separatrix between stable and plunging orbits. The relevant functions are:

KerrGeoISCO[a,x]
KerrGeoISSO[a,x]
KerrGeoPhotonSphereRadius[a,x]
KerrGeoIBSO[a,x]
KerrGeoSeparatrix[a,e,x]

Further examples

See the Documentation Centre for a tutorial and documentation on individual commands. Example notebooks can also be found in the Mathematica Toolkit Examples repository.

Citing

In addition to acknowledging the Black Hole Perturbation Toolkit as suggested on the front page we also recommend citing the specific package version you use via the citation information on the package’s Zenodo page linked from the above DOI.

Authors and contributors

Niels Warburton, Maarten van de Meent, Zach Nasipak, Thomas Osburn, Charles Evans, Leo Stein, Philip Lynch, Oliver Long